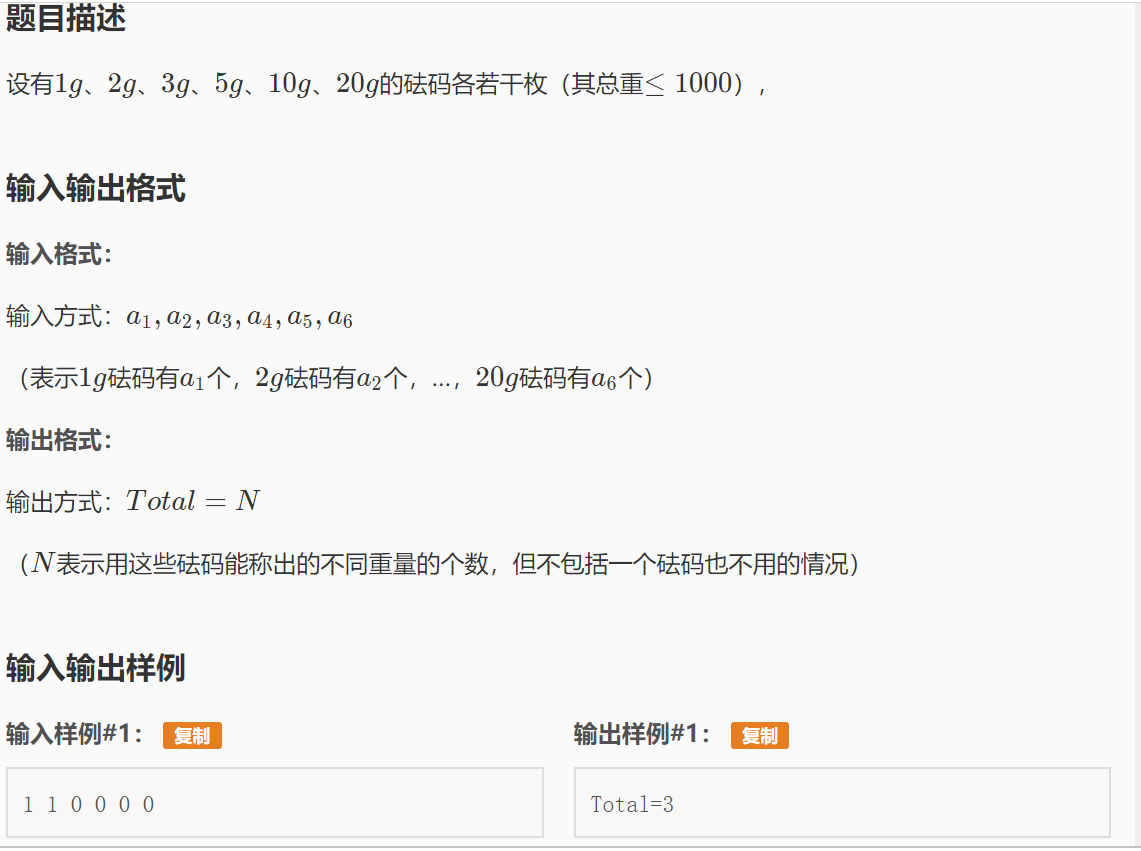
可以转化为01背包求方案数的问题,dp数组f[][]表示第几个砝码能称出的重量,可压缩至一维 转移方程为f(i,j)+=f(i-1,j-w[i]) 当前我们可以称出的重量必定是由之前的砝码重量转移过来的
#includeusing namespace std;const int N=550;const int maxn=1e6+7;int f[maxn];int a[maxn];int v[maxn];//相当于01背包的物品重量int num[10]={ 0,1,2,3,5,10,20};//砝码重量int cnt; int maxsum;int ans;int main(){ for(int i=1;i<=6;i++) { scanf("%d",&a[i]); for(int j=1;j<=a[i];j++) { v[++cnt]=num[i];//统计 } } for(int i=1;i<=cnt;i++) { maxsum+=v[i];//背包的最大容量 } f[0]=1;//0也是一种方案,初始状态 for(int i=1;i<=cnt;i++)//01背包 { for(int j=maxsum;j>=v[i];j--) { f[j]+=f[j-v[i]]; } } for(int i=1;i<=maxsum;i++)//统计方案个数 { if(f[i]) { ans++; } } printf("Total=%d",ans); return 0;}